The assignment 8 is the implementation of the AVL trees. We have to use the previous BST tree and add on the rotation methods to it.
AVL trees have the property that the difference of the height of left subtree and the height of the right subtree should be no more than 2 and this
is true recursively. If the height exceeds, then the tree is unbalanced at that node and rebalancing is required. Depending upon where it is
unbalanced, the different rotations have to be applied.
Different parts of the assignment are:
- We need to implement the AVL tree. We need to write the insert() and delete() methods such that when we insert elements we need to balance the
tree if required.
- For BST, we calculated the height recursively, the time complexity is O(n). The insertion and deletion is O(log n). As we know we need
to calculate the height of the right and left subtree and if do it recursively, then the insertion and deletion is O(nlogn) which
takes more time than usual. So our task is to perform the insertion and deletion in O(log n ). This is achieved by calculating the height
in constant time.
When you create a new node or when you insert an element, initially the height is set to 0 and after we insert, while
we go up the tree, we simply update the height at every node as the sum of height of left and right subtree. So, in this way when we want
to calculate the condition for balancing, we simply do it in constant time and if needed, we balance the tree.
We need to add an
additional field i.e height of the type 'int' which stores the height of each node.
- We need to compare the AVL trees with Binary Search Tree and draw out some conclusions with some graphs.
The graphs I have posted below:
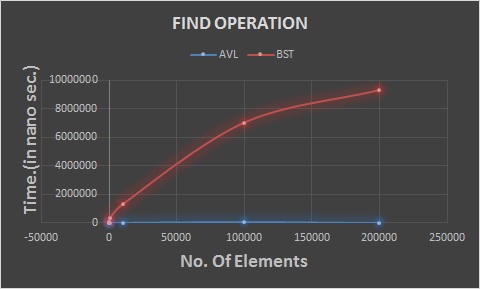
- As we can see, the find operation is performed much faster by AVL trees than by the BST trees. The reason is, the AVL tree is a self-
balancing trees and so the height is as small as possible. So the element is found is immediately.
-
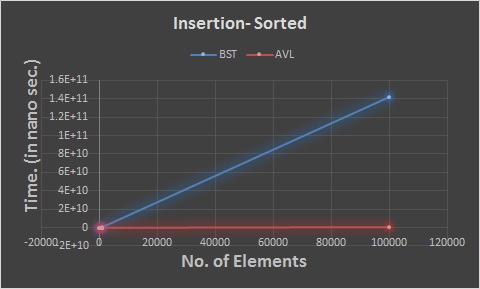
The insertion of elements in sorted order is done faster by the AVL tree. Depending upon the elements being added in ascending or descending
order, the elements are added either on the left or the right side. In either case, when more than two elements are added, rebalancing is done
which results in the decrease of the height of the tree. But, in BST the elements are added from one side, which results in the tree being
heavy from one side. So whenever new element is added, the element has to go further a lot below the tree to reach the end of the tree where the
element is added.
- Comment interesting parts of the program so that any other programnmer looking at my code has a good understanding of what I am trying to do.
- I would be graded on how elegant my program is.
- We have to create a webpage for it.
- The written HW as well is very important and has got a few tricky Questions.
Which Tree is faster.? AVl tree or BST tree.?
- As we can see from the graphs, the AVL tree is much faster than the BST when we want to find a number in a large set of numbers.
- The insertion is faster in AVL tree.
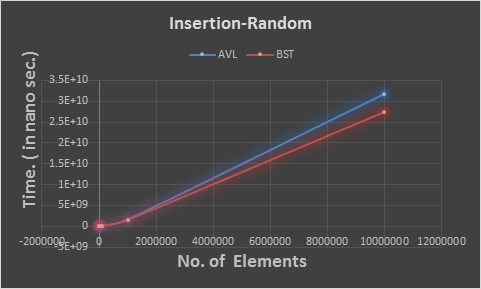
Can you find any input for which the BST is faster than the AVL tree.?
Ans. Clearly, when we are inserting the random elements in AVL tree it takes a little more time than what the BST trees take.
Maybe the AVL takes slightly more time in rotations. The BST performs a bit faster than the AVL tree when we are inserting random numbers in BST.
Thus, inserting random elements is the input where the vanilla BST is faster than the AVL tree.
The graph for this is posted below :

My conclusions for the AVL trees are as follows:
- The AVL tree is faster than the BST.
- When we know that we have to do more searching than insertions, we should without any doubt use AVL trees.
- The insertions into AVL trees make take more time than in BST when random elements are inserted, but that is quite a minute difference.
- The AVL trees has more practical applications than in BST because of its balancing property and thus it can be used in real-world applications.
ThankYou.!


