Assignment 5:

Assignment 5 is about different sorting algorithms. We have to implement 5 different sorting algorithms and study the time complexities for each of them and draw graphs and write down conclusions on them.

1. Bubble Sort

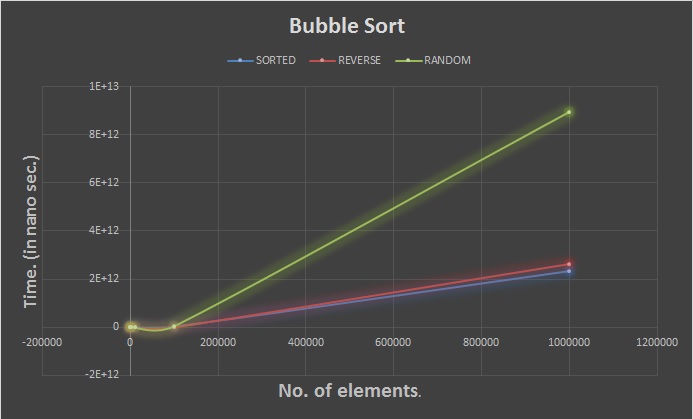
   Bubble sort is an algorithm which is the simplest algorithm of all.

   In this algorithm every element is compared with the next element and if the two are not in the proper order they are swapped. In this way the largest element is at the end of the array. There are n comparisons required to push the largest element at the end of the array. Theses n comparisons have to be done n times for locating the current largest element and push to the end of the list.

   Time complexity:

   • If the list is already sorted there are no swaps and the algorithm will run for only n times.So for the best case:O(n)
   • If the list is sorted in the descending order i.e. it is sorted in the reverse order , it is the worst case and the time complexity is:O(n²)
   • The average time complexity for bubble sort is:O(n²)

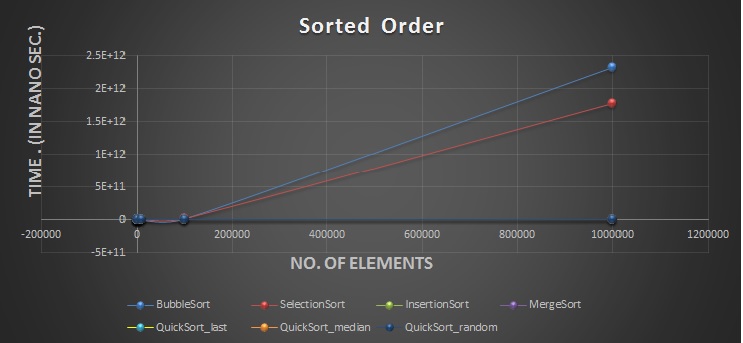
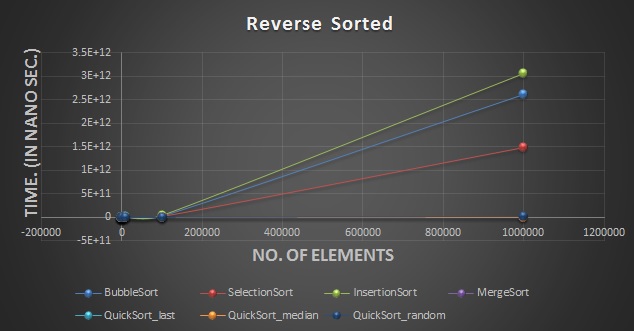
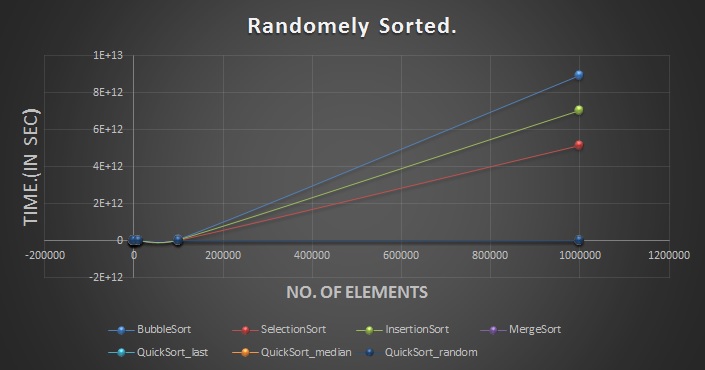
   The graphs for the Bubble sort for the various cases(sorted,reverse sorted and randomly sorted) is posted below:

   
2. Selection Sort

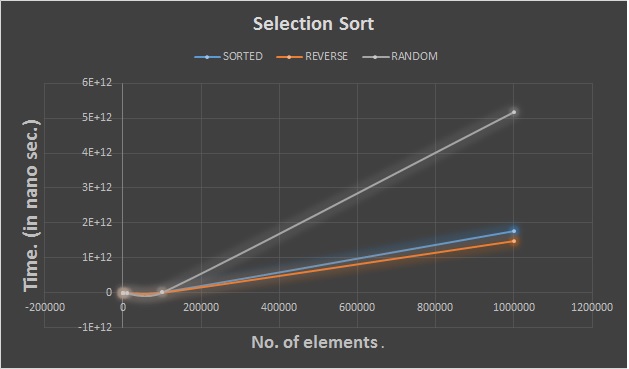
   In this sorting algorithm we divide the list into two parts: one is sorted and the other is unsorted. Initially the entire array is an unsorted array. We find the minimum element in the array and place in the current position of the unsorted array. Now we move the range of the unsorted array by one and then find next minimum element and place in the current first position of the unsorted list and continue the process till sorted array reaches till the end.

   Time complexity:

   • No matter how the data is arranged there would always be comparisons and swaps made and so the time complexity for best,average and worst case is : O(n²)

   The graphs for the Selection sort for the various cases(sorted,reverse sorted and randomly sorted) is posted below:

   
3. Insertion sort

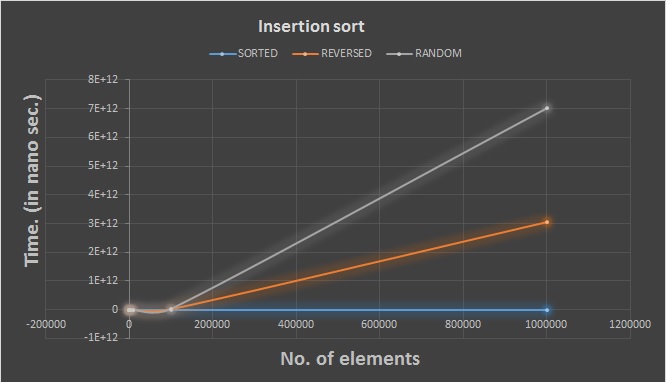
   This sort is more efficient than bubble sort and selection sort. In this algorithm we divide the entire array into two parts: the sorted array and the unsorted array. With every iteration we have to place the first element of the unsorted array in the correct position of the sorted array and increase the sorted list by one.

   Time complexity:

   • When elements are sorted, there are no swaps and the correct position of the element in the sorted list is the current index itself. The time complexity is : O(n)
   • When the elements are sorted in the reverse direction,there will always be swaps in proportion to the number of elements currently in the sorted list.The time complexity is: O(n²).This is the worst case.
   • The average case time complexity is:O(n²)

   The graphs for the Insertion sort for the various cases(sorted,reverse sorted and randomly sorted) is posted below:

   

Divide and Conquer approach

In this approach the algorithm is divided into multiple sub-problems. Each of these sub-problems is then solved seperately and the solution of each sub-problem is used to solve the original problem. Divide and conquer technique uses recursion to solve each of the sub-problem.

4. Merge Sort.

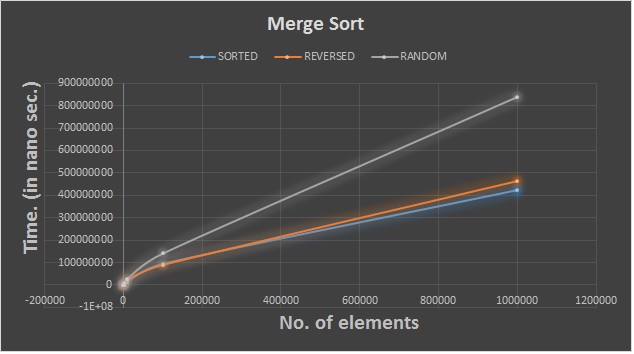
   Merge sort uses the divide and conquer approach. It is one of the most efficient algorithm for sorting. In this algorithm, we divide the list into two from the middle and keep dividing the list until the sub-problem has only one element list.

   We then merge the list and while merging the list we sort them in the ascending order.

   Time complexity:

   • We are dividing the list into two no matter if the list is sorted or no. But if the array is sorted, while merging the list there are no swaps merging results into an array itself. Thus, the best, average and worst case time complexity is: O(nlogn)

   The graphs for the Merge sort for the various cases(sorted,reverse sorted and randomly sorted) is posted below:(post here)

   
5. Quick Sort

   The quick sort uses the similar approach of divide and conquer technique.

   In this technique, a element is selected which is the pivot element. Now the elements which are less than the pivot are placed to the left of the array and the element which are more than the pivot are placed to the right of the pivot.The index of the pivot element is then returned back to the function. The same function is called to the sub-array left to the pivot which has all the elements less than the pivot and also to the right of the sub-array which has the elements more than the pivot.

   After calling the function recursively, the resulting function will be a sorted array

   Time complexity:

   • The best case is when the elements are in a sorted manner. The best and average case time complexity is : O(nlogn)
   • The worst case time complexity is when the elements are in a reverse sorted manner. The time complexity is: O(n²)

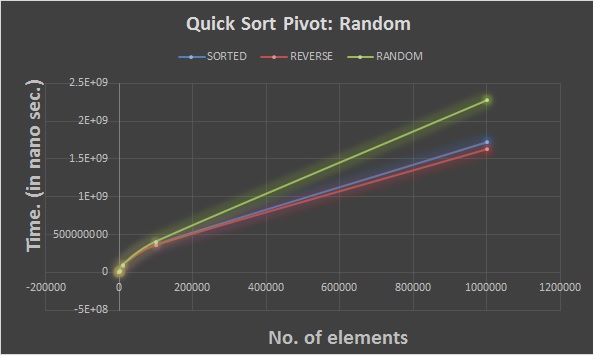
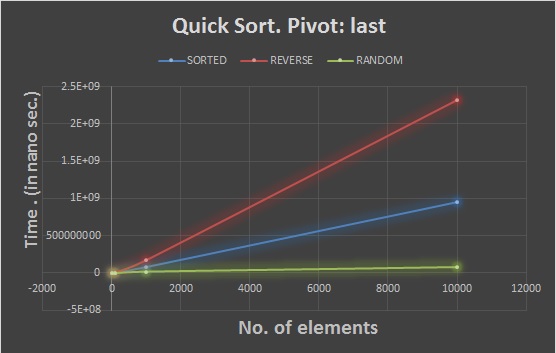
   The graphs for the Quick Sort for the various cases(sorted,reverse sorted and randomly sorted) for different choices of the pivot is posted below:(post here)

   1. Quick Sort. Pivot:last

      In this Quick Sort, the last element in the list is taken as the pivot element. This Quick Sort is a bit slow as compared to other approaches of Quick Sort.

      

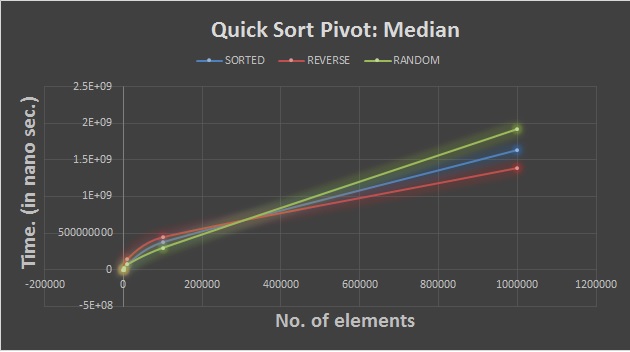
   2. QuickSort. Pivot:median

      In this Quick Sort, the median of the start,end and the middle is taken as the pivot element. This approach is faster than the last pivot approach. In fact, this is the fastest of all three aproaches.This approach gives a linear time complexity.

      

   3. Quick Sort. Pivot:Random

      In this Quick Sort, any random element from the list from start to end is taken as the pivot element.This is good appraoch but may fail at times and may give exponential time

      

My observations and comments on basis the graphs and the readings:

1. Sorted List
   • The selection sort and bubble sort performs the worst for this arrangement.
   • Insertion sort performs a bit better.
   • Merge Sort performs the best.
   • Quick sort-median and Quick sort-random are pretty good

   

2. Reverse Sorted
   • Selection sort,Bubble Sort, Insertion sort take a lot of time to sort large numbers. All these sorting should be avoided.
   • Merge Sort is pretty fast.
   • Quick sort is also very fast.Only the pivot-median and pivot-random should be employed.The pivot-last approach is quite slow approach.

   

3. Randomely Sorted
   • For this approach.Most of the times this is going to be the approach since we are going to sort random numbers.
   • Bubble sort,Selection Sort, Insertion Sort should never be emplyed. They take hours to sort a million elements. You can see that by the readings provided in the zip file of the assignment 5 folder.
   • Merge sort performs very well for this sort. It should be employed.
   • Also the quick sort algorithm performs very well for a million elements.All three approaches of quick sort are pretty fast and any of them can be employed. However, if one requires very good efficiency, he should use Quick Sort pivot- median approach.

   

On basis of the readings, I have concluded:

• Bubble sort,selection sort,insertion sort should never be employed for sorting numbers having size of more than or equal to 100000
• Merge sort can be employed for any number of elements and it is the best from among all of them
• Quick Sort is also very fast. But if this employed the quick sort pivot -random or pivot - median should be used.