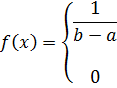Computational Statistics
CS 5961/6961
Basic Statistics Definitions
- Probability density function
- Discrete: If X is a discrete random variable with possible values x1, x2, x3, ...,
xn, and f (xi ) denotes P ( X = xi ), the probability that the
value of X = xi , then f is called the (discrete) probability density function (pdf), or simply the density function for X .
Note that, for all x , f (xi ) ≥ 0 and ∑i f (xi) = 1 , where the elements are summed over all i .
- Continuous: If X is a continous random variable, then the (continuous) probability density function is defined as
that function f such that when integrated as below, gives the probabaility that X < a , for some constant a,
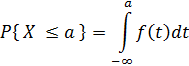
- Cumulative density function
- Discrete:
- Continuous:
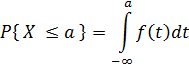
- Uniform distribution function
- Discrete: A uniform probability space is a finite space in which all the outcomes have the same probability. That is, if X is a discrete random variable with event space {x1, x2, x3, ..., xn}, and f (xi ) denotes P ( X = xi ), then the probability that the value of X is xi , is simply 1/n .That is, for all i, 1 ≤ i ≤ n , f (xi ) = 1/n
- Continuous: Let X be a continous random variable and X ∈ [a,b]. Then the (continuous) uniform probability density function f is defined by
- Binomial distribution function
- Normal or Gaussian Distribution
- Convolution
- Discrete:
- Continuous:
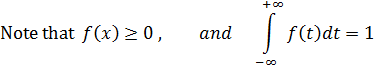
| |
||
|
for |
|
|
otherwise |
|