Due: Friday, October 21st, 2011 10:45am
Start with mini-dr.rkt, which needs string.rkt in the same directory.
The initial Mini DrRacket works only with number values, plus, and minus. Add times:
(check-expect (eval-expr '(* 2 3)) 6)
To suport conditionals, we could add booleans to the set of expressions and values. It’s easier, however, to add an if0 form that looks for 0 instead of true.
Add an if0 form to the expr datatype so that the following examples are allowed, and then adjust eval-expr to make the examples work:
(check-expect (eval-expr '(if0 0 2 3)) 2) (check-expect (eval-expr '(if0 1 2 3)) 3) (check-expect (eval-expr '(if0 (- 8 8) 2 3)) 2)
Extend the set of expressions to include variables, where a variable is represented by a symbol. For now, using a variable simply triggers an error by using the error function. You can test for an error using check-error.
(check-error (eval-expr 'x)) (check-error (eval-expr '(+ 1 x)))
Hint: It’s eaisest to add variables to you data definition right after numbers, so that later tests for the other forms can assume that the expression is represented by a list.
Create a new function (that is not connected to the GUI, for now) called subst. The subst function takes an expression, a symbol (representing a variable), and a number. It returns an expression like the given one, except that every use of the given variable is replaced by the given number.
(check-expect (subst '(+ 1 x) 'x 3) '(+ 1 3)) (check-expect (subst '(+ 1 y) 'x 3) '(+ 1 y)) (check-expect (subst '(if0 (+ 1 y) x y) 'y 10) '(if0 (+ 1 10) x 10))
Note that you’ll need more examples/tests for subst than the ones given above.
A function of one argument always has the form
(define (name arg) expr)
which suggests the data defintion
;; A func is ;; (list 'define (list sym sym) expr)
Implement the function lookup, which takes a list of funcs and a symbol. The lookup function returns a func whose name matches the given symbol. If no matching function exists, lookup should report an error.
Extend the definition of expr to including function calls:
;; An expr is either ;; .... ;; - (list sym expr)
Assume that a function name is never +, -, or if0, so that this new case in the definition of expr does not overlap with the other cases.
Adjust your eval-expr function to accept an expression and a list of funcs:
;; eval-expr : expr list-of-funcs -> num
For now, you can adjust the GUI to pass empty as the list of function definitions.
The list of funcs for eval-expr is mostly along for the ride, but to implement the case of function calls, eval-expr will need to use lookup to find a function in the list of funcs, and it will need to use subst to put the argument value in place of the function argument in the body of the found function.
(check-expect (eval-expr '(f 1) (list '(define (f x) (+ x 2))))
3)
(check-expect (eval-expr '(g (+ 3 4)) (list '(define (f x) (+ x 2))
'(define (g y) (f (- y 3)))))
6)
(check-expect (eval-expr '(fact 5) (list '(define (fact x)
(if0 x
1
(* x (fact (- x 1)))))))
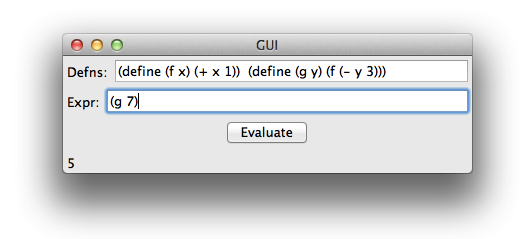
120)Add a new field to the GUI before the expr field. The new field accepts a sequence of definitions. A user of the GUI will have to type all the definitions on a single line, which is annoying, but that could be easily fixed with a slightly fancier GUI library. Your GUI will look like this:

Use many-from-string to convert the content of the definitions text field to a list of funcs, then pass that list as the second argument to eval-expr.
Add lambda forms (with a single argument) to the set of expressions. A lambda form is a value:
(check-expect (eval-expr '(lambda (x) (+ x 1)) empty)
'(lambda (x) (+ x 1)))Generalize function calls to allow an arbitrary expression (instead of just a function name) as the function to call:
(check-expect (eval-expr '((lambda (x) (+ x 1)) 8) empty)
9)Hint: For the cases of expr, it’s easier to use equal? at this point instead of symbol=?, because the first sub-expression in a function call is not always represented as a symbol.
You will also need to adjust the way that eval-expr handles variables: instead of reporting an error, the value of a variable should be a function from the list of funcs given to eval-expr (if there is a function with a matching name), but converted to lambda form:
(check-expect (eval-expr 'f (list '(define (f x) (+ x 1))))
'(lambda (x) (+ x 1)))Finally, adding lambda complicates subst. If subst is given '(lambda (x) (+ x 1)) and asked to replace every 'x with 7, then it should leave the lambda form alone, because the x for the lambda argument must be a different x than the one that is being replaced. More generally, subst should leave a lambda alone when the name of the lambda’s argument matches the name that is being replaced.
(check-expect (subst '(lambda (x) x) 'x 10) '(lambda (x) x)) (check-expect (subst '(lambda (y) x) 'x 10) '(lambda (y) 10))
Adding lambda to your interpreter makes it extremely powerful, although that may not be immediately apparent. It turns out, for example, that you can encode lists using lambda without explicitly adding support for lists to your interpreter. Below is a stress test for your interpreter that defines and encoding of lists and uses it to sum the numbers in a list containing 8 and 17. (The calls to cons and other functions look funny, because we have only single-argument functions, so we curry a two-argument function to make it a function of one argument that returns a function for the second argument.)
(define defns
(list
;; Encode `cons', `first', `rest', `empty', and `empty?'
;; using functions:
'(define (pair a) (lambda (b) (lambda (p) ((p a) b))))
'(define (fst v) (v (lambda (a) (lambda (b) a))))
'(define (snd v) (v (lambda (a) (lambda (b) b))))
'(define (empty p) ((p 0) 0))
'(define (cons a) (lambda (b) ((pair 1) ((pair a) b))))
'(define (empty? x) (fst x))
'(define (cons? x) (- (fst x) 1))
'(define (first c) (fst (snd c)))
'(define (rest c) (snd (snd c)))
;; Implement `sum' using `empty?', `first', and `rest':
'(define (sum l)
(if0 (empty? l)
0
(+ (first l) (sum (rest l)))))))
;; Call the `sum' function:
(check-expect (eval-expr '(sum ((cons 8) ((cons 17) empty)))
defns)
25)| Last update: Friday, November 4th, 2011mflatt@cs.utah.edu |