ECE 5340/6340††††††††††††††††††††††††††††††††††††† NUMERICAL INTEGRATION††††††††††††††††††††††††† Page 1
a) TRAPEZOIDAL INTEGRATION
![]()
![]()
![]()
![]()
![]()
![]() †††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††
††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† ![]() ††
††
![]()
![]()
![]()
![]()
![]() †††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††
†††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††
![]() ††††††††††††††††††††††††††††††† ††††††† ††††††††††††††††††††††† †††††
††††††††††††††††††††††††††††††† ††††††† ††††††††††††††††††††††† †††††![]() †††††††††††††††††††††† †††=† Area under curve
†††††††††††††††††††††† †††=† Area under curve
††††††††††††††††††††††††††††††† ††††††† ![]()
††††††† Numerical Integration approximates the curve by a† function and integrates this new approximate function.
††††††† Trapezoidal integration approximates the function by a line (1st order† polynomials).
![]() ††††††††††††††††††††††††††††††††††††††††††††††† ††††††††† Error
††††††††††††††††††††††††††††††††††††††††††††††† ††††††††† Error
![]()
![]()
![]()
![]() ††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† †††††† Straight lines are approximations of
curved function f(x)
††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† †††††† Straight lines are approximations of
curved function f(x)
![]()
![]()
![]() †††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††
††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† ![]()
![]()
![]()
![]() ††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† h†††††††††††††
††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† h††††††††††††† ![]()
††††††††††††††††††††††††††††††††††††††††††††††† ![]() ††††††††††† †
††††††††††† † ![]() †††††††††
†††††††††
††††††††††††††††††††††††††††††† ††††††
††††††††††††††††††††††††††††††† Calculate the area under each trapezoid
![]()
![]()
![]()
![]()
![]()
![]()
![]() †††††††††††††††
††††††††††††††† ![]() ††† ††
††† †† ![]() ††
†† ![]() ††††
††††![]() †††††††††††††††††††††† Area
†††††††††††††††††††††† Area![]() =
= ![]()
![]() ††††††††††††††††††††††††††††††††††††††††††††††† †††††††††
††††††††††††††††††††††††††††††††††††††††††††††† ††††††††† ![]()
††††††††††††††††††††††††††††††† †††† ![]() ††††††
††††††![]() †††††††
†††††††![]()
††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† Area![]() =†
=† ![]()
†††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††
††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† Area†††† =† ![]()
††††††††††††††† TRAPEZOIDAL
RULE
††††††††††††††† 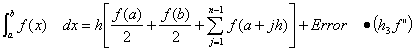
††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† Assuming equal-spaced points
ECE5340/6340†††††††††††††††††††††† NUMERICAL INTEGRATION††††††††††††††††††††††††††††††††††††††††† PAGE 2
SIMPSONíS INTEGRATION
Approximate ![]() †by a set of 2nd
order LaGrange Polynomials
†by a set of 2nd
order LaGrange Polynomials
![]()
![]()
![]()
![]()
![]() †††††††
††††††† ![]() †††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††
†††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††
††††††††††††††††††††††††††††††††††††††††††††††† ††††††† ![]() †††††††††††††††††††††††††††††††††††††††††††††††††††
†††††††††††††††††††††††††††††††††††††††††††††††††††
![]()
![]() ††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† †††††††
††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† ††††††† ![]() †††††††††††††††††††
†††††††††††††††††††
††††††††††††††††††††††††††††††† †††††††† ![]() †††††
†††††![]() †††††
†††††![]() ††††††
††††††
††††††††††††††††††††††††††††††† ††††††††††††††††††
LaGrange Polynomial:
![]()
![]()
††††††††††††††† ![]()
Third order derivatives cancel out for equal-spaced points.
SIMPSONíS RULE
![]()
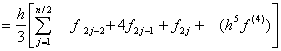
††††††††††††††† Break region into even # of regions using odd # of points†††††††††
Alternative form of algorithm:
![]()
To Calculate Expected Error for Realistic Simulation:
For Trapezoidal Integration, error is ON THE ORDER OF h3 f ''
For Simpson Integration, error is on the order of h5 f (4)
BUT we don't know the derivatives f '' and f (4).
To approximate these
(a) Most accurate, most work:† Calculate the derivatives of f(x) at the central location of each region (x= h/2, 3h/2, 5h/2, etc., and average these derivatives.† The derivatives must be calculated numerically, because we assume we do not know f(x)† (If we did, we could usually find a way to integrate it).†
(b) Less accurate, less work:† Calculate the derivatives at an average location (x = a + (b-a)/2)
(c) Even less accurate, even less work, most likely to be used in practice:† If you have an idea what the order of the derivative is from the physical understanding of your application, use that.† Otherwise, assume the derivative is on the order of 1.
For HW assignment #1, when you are asked to find the approximate error, use method b and compare with method c.† IF you had only numerical data and could not calculate the derivative analytically, which of these methods would you be satisfied with?
Some tempting stumbling blocks:
What do you do with a knowledge of the error?† How about subtracting it from your solution to get a better answer?† No, don't do this.† You only know the ORDER of the error, and it could be either positive or negative, and won't be exactly what you calculate.† Use this ONLY to determine the decimal place or degree or accuracy of your solution.
2-D INTEGRATION (TRAPEZOIDAL METHOD)††††††
††††††† 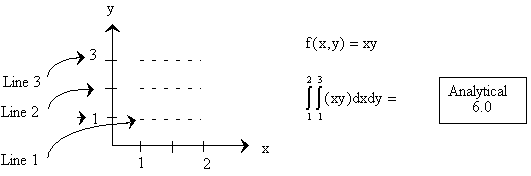
††††††††††††††† Let
††††††††††††††††††††††††††††††††††††††††††††††† nx = ny †= 2†††††††††††††††††††††††††††† hx = (2 - 1)/2 = 0.5
Line 1)††† y = 1†††††††††††††††††††††† f1(x) = x†††††††††††††††††† hy = (3 - 1)/2 = 1
††††††††††††††††††††††††††††††††††††††††† 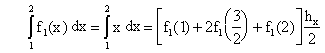
††††††††††††††††††††††††††††††††††††††††††† ![]()
Line 2)††† y = 2†††††††††††††††††††††† f2(x) = 2x
††††††††††††††††††††††††††††††††††††††††† ![]()
†††††††††††††††††††††††††††††††††††††††††††††††††††††† ![]()
Line 3)††† y = 3†††††††††††††††††††††† f3(x) = 3x
††††††††††††††††††††††††††††††††††††††††††††††† ![]()
†††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† ![]()
††††††††††††††††††††††††††††††† ![]()
†††††††††††††††††††††††††††††††††††††† 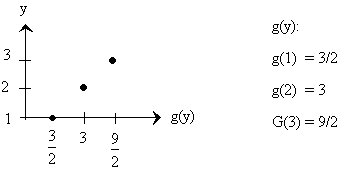
†††††††††††††††††††††††††††††††††††††††††††††††††††††††††† ![]()
††††††††††††††††††††††††††††††††††††††††††††††††††††† ![]()
††††††††††††††††††††††††††††††† ![]()
††††††††††††††††††††††††††††††† ![]()
Note:††††††††††††††††††††† You would have obtained identical results by:
††††††††††††††††††††††††††††††††††††††††††††††††††††††††