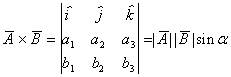ECE 5340/6340: Lecture 4 -- REVIEW OF MATRIX ALGEBRA

Why matrix equations are important in numerical methods:

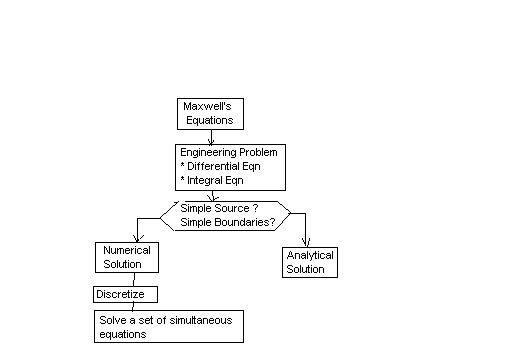
SIMULTANEOUS EQUATIONS: are of the form

a₁₁ x₁ + a₁₂ x₂ + a₁₃ x₃ + … + a_1n x_n = b₁

a₂₁ x₁ + a₂₂ x₂ + a₂₃ x₃ + … + a_2n x_n = b₂

a_m1x₁ + a_m2 x₂ + a_m3 x₃ + … + a_mn x_n = b_m

Which can be written as a matrix equation:

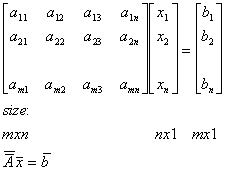
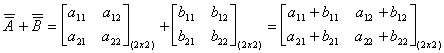
MATRIX ADDITION:

MATRIX TRANSPOSE:

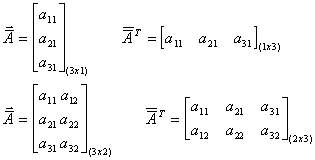
INNER OR DOT PRODUCT

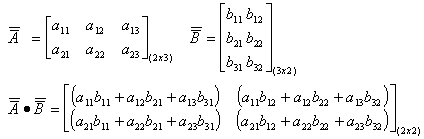
VECTOR DOT PRODUCT

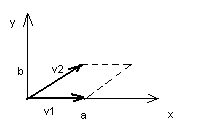
p = v₁·v₂ = component of v₁ in v₂ direction = |v₁||v₂|cos(a)

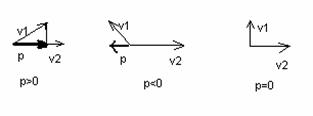
(a = angle between vectors)

DETERMINANT of a matrix (as it relates to matrix singularity)

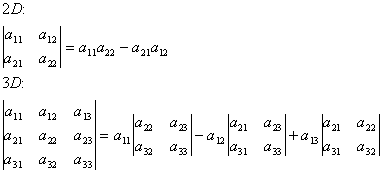
4D: Repeat.

Method:

1) Find minor matrices by striking row and column.

2) Multiply by element

3) Signs alternate +-+-+- …

Determinant: Defines the “hypervolume” of a matrix.

2x2 : area defined by parallelogram of matrix vectors

3x3 : volume defined by parallelopiped of matrix vectors

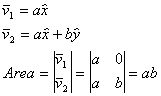
· If any two vectors become coincident (2D: parallel / 3D: in the same plane), then the area or volume collapses to zero.

· If you are solving 3 equations in 3 unknowns, you can only solve it if your equations (vectors) are independent (not coincident).

· Thus, if the determinant of the matrix is zero (or near zero), you cannot solve the matrix equation.

· This is called a “singular matrix”.

DIAGONAL MATRIX

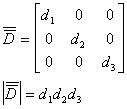
IDENTITY MATRIX

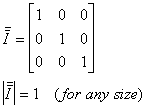
TRIANGULAR MATRIX

DETERMINANT OF PRODUCT OF MATRICES:

BANDED MATRIX:

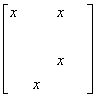
SPARSE MATRIX:

VECTOR CROSS PRODUCT