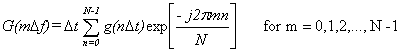Faster than Fourier –
Ultra-Efficient
Time-to-Frequency Domain Conversions for FDTD Simulations
Cynthia
M. Furse, Department of Electrical and Computer Engineering
E-mail:
furse@alpha.ece.usu.edu
Phone:
(435) 797-2870, Fax: (435) 797-3054
Keywords: FDTD methods, Computation time, Frequency
domain analysis, Time domain analysis, Discrete Fourier transforms
Abstract
This tutorial compares several
methods of converting from the time-to-frequency domain for FDTD
simulations. Applications include
calculation of field or power distribution, antenna impedance and radiation
pattern. The traditional fourier transform methods are compared to two methods based
on the solution of linear equations. This tutorial describes how to program and
use these techniques, and evaluates their effectiveness for several
applications including analysis of a millimeter-resolution human model
underneath a 60-Hz power line, antenna radiation pattern and impedance
calculations, calculation of coupling of a cellular telephone to the human
head, and geophysical prospecting simulations.
1. Introduction
Many
applications of the finite-difference time-domain (FDTD) method require
conversion of time-domain field data to frequency domain data (magnitude and
phase) over large regions of the model.
Applications include bioelectromagnetic dosimetry calculations of the
human body for analysis of cellular telephones [1-4], power lines [5,6], and
other EM-safety studies [7], antenna impedance and radiation patterns [8],
radar cross section calculations [9], and calculations of S-parameters of
microwave circuits [10]. Time-to-frequency domain conversions have
traditionally been done with either the fast fourier
transform (FFT) [11-12] or the discrete fourier transform (DFT) [13-14]. When multiple frequencies are of interest,
the FDTD method is commonly used with a pulsed excitation, and the fourier transform methods are used to obtain the desired
results at these frequencies. More
recently, methods based on the solution of linear equations have been found to
be more efficient than the fourier transform methods
[15].
This
tutorial compares the traditional fourier transform
methods and methods based on solution of linear equations for time-to-frequency
domain conversions for FDTD simulations.
Equations are given for computing memory and computational requirements
for individual applications. In
addition, the use of these methods for specific electromagnetic applications is
discussed.
A brief
outline of the computational aspects of the FDTD method is given in Section
II. Section III briefly describes the fourier transform methods and their computational
requirements. It also describes methods
that have been used to optimize the fourier
methods. Section IV describes two
methods based on linear equations that can be used in place of fourier transform methods.
The first of these methods is the two-equations
two-unknowns (2E2U) method that can be used for single-frequency FDTD
simulations. The second of these methods
is its extension to multiple frequencies, called the N-equations and N-unknowns
(NENU) method. Section V gives examples
of the types of calculations that are needed in realistic applications and
compares the computational requirements and relative advantages of each of the methods,
with the hopes of providing the user with guidance for choosing the optimal
method for a specific application.
II. Computational Aspects of the FDTD Algorithm
The
FDTD algorithm has been described in detail in available literature, [16,17] so it will not be described here. The general forms of the FDTD equations for
the three electric field components (Ex, Ey, Ez) and three magnetic field components (Hx,
Hy, Hz,) are shown below:
Ex(i,j,k) = Ex(i,j,k) + C1 (Hz(i,j,k) – Hz(i,j-1,k)
+ Hy(i,j,k-1) – Hy(i,j,k)) (1)
Hx(i,j,k) = C2 Hx(i,j,k) + C3
(Ez (i,j,k) – Ez(i,j+1,k) + Ey(i,j,k+1) - Ey(i,j,k))
where the
constants C1, C2, and C3 depend on the
electrical properties of the material at each point (i,j,k) in the model. The number of real
multiplications required for computing this algorithm per time step are:
Number of
multiplications =
9 Nxyz
where
Nxyz is the
number of FDTD cells = NxNyNz
For the purposes of this tutorial, additional computational overhead for initialization of the simulation, boundary conditions, and incidental calculations will be neglected. In practice, it is common for boundary conditions to take 10 to 30% of the total computational time, depending on the simulation size and boundary conditions used, so these computational costs are not necessarily negligible in practice. They are neglected here because they have no effect on or from the time-to-frequency domain conversions, which is the topic of this paper.
The storage requirements for the FDTD simulation (again neglecting boundary conditions and incidental storage) is one real value for each of the six vector field components and one for an integer indicating what dielectric material exists at each FDTD cell location:
RAM required for FDTD = 7 Nxyz
Disk required for FDTD = 0.
These
values are shown in Table 1, which is used throughout this tutorial to
summarize computational requirements.
III.
Fourier Transform Methods (DFT or FFT)
Fourier transform methods are the traditional methods of converting from the time to frequency domains for most discrete applications including FDTD. They are very accurate, can be used with either single or multiple frequency simulations, and there are numerous commercial software packages available for making these calculations.
The discrete fourier transform (DFT) [18] is based on a running summation
of the time domain field as given below:
|
|
where
G(mDf) = the complex value of the magnitude and
phase of the equivalent steady-state sine wave at frequency mDf
g(nDt) = the time-domain
value of the pulse at time nDt
N = length of the fourier
transform = 1/ (Df Dt)
Df = the frequency resolution of the frequency-domain
calculations
m =
the frequency index, m=0,1,2,...,N-1
Dt = the sampling period of the DFT
Normalization is normally
required in order to obtain frequency domain data equivalent to the magnitude
and phase of a 1 V/m incident sine wave at each frequency of interest. Since commonly-used pulse shapes do not have
constant frequency responses, the final values must also be normalized by
(divided by) the complex DFT of the incident pulse. This normalization step can be eliminated by
used a step-function which has a constant (unity) frequency spectrum [15,33]. Numerical
dispersion in the FDTD grid eliminates the high frequencies, so they do not
cause aliasing errors or otherwise interfere with the solution. Since the normalization requires only a
single fourier transform which is reused for all
points in the grid, the choice of pulse shape and the issue of normalization
has negligible effect on the computational requirements of the simulation.
The computational requirements of the DFT are:
Number of (complex) multiplications =
NFDTDNPxyzNPNF
where
NFDTD = Number of time steps in the FDTD simulation
NF = Number of
frequencies of interest (number of DFT summations)
NP = Number of
Parameters of Interest (six vector field components, for instance)
NPxyz = Number of points of interest (such
as all locations within the grid, for complete field distributions, a set of
surfaces for radiation pattern, or a few isolated points for impedance
calculations)
The storage requirements of the DFT are:
RAM required for DFT = 2NPxyzNPNF
Disk required for DFT = 0.
This assumes that the DFT summation is computed as a running sum inside the FDTD code, rather than storing all of the time domain values for later processing with commercial software. In practice, disk storage and later computation with commercial software is only possible when a very limited number of time-to-frequency conversions are of interest (such as impedance calculations). For problems requiring fourier transforms for surfaces or volumes of points, the storage requirements (either RAM or disk) become prohibitively large.
The fast fourier transform (FFT) was developed as an efficient method
of computing the fourier transform.[18] The complete time history of the values at
all points of interest is stored, and the exponential components are computed
iteratively. In the Radix-2 algorithm, a
commonly-used algorithm because of its high efficiency, the length (N) of the fourier transform is 2n. Most FDTD simulations are run for some
arbitrary number of time steps, not necessarily 2n. This is not a problem however, as the FDTD
pulsed data can be padded with zeros to create an array with length suitable
for the Radix-2 algorithm. However, even
with the use of the Radix-2 algorithm, the FFT has been shown to be computationally
more expensive than the DFT for all FDTD simulations. [19]
One of the limitations of the traditional FFT has been that it requires
evenly-spaced data (not suitable for exponentially increasing time steps), and
that it produces evenly-spaced frequency data (difficult to obtain exactly the
frequencies of interest). This limitation has been partially solved by the use
of the unequal-spaced FFT. [20] The
storage and computational requirements are similar, however, so this method is
not useful for FDTD simulations requiring a large number of time-to-frequency
domain calculations.
Desampling
has been used to minimize the computational requirements of fourier transform
computations.[14]
This minimizes the number of FDTD samples used to obtain the fourier
transform. Since FDTD calculations are
oversampled according to the Nyquist criterion [14,19],
not all of them are required for fourier transform calculations. If, for instance, only every tenth FDTD
sample is chosen for computation of the fourier
transform, the computational requirements of the fourier transform are divided
by ten. This method still relies on the
samples being evenly spaced, and requires storage of the running sum, so the
memory requirements are the same as for the DFT. Desampling rarely improves the efficiency of
the fourier transform by more than a factor of 10.
Fourier
transform methods are limited for use in low frequency high resolution
simulations (such as analysis of a millimeter resolution model of the human
body under a 60 Hz power line), where the sampling resolution of the wave form is ultra high.
For single-frequency (CW) simulations, the fourier
transform calculations must be made over a full half-cycle of the converged
sine wave. This requires at least an
additional half-cycle of FDTD calculations, which can be difficult or
impossible for low frequency calculations, and which increases the cumulative
error inherent in the finite-difference calculations.
The computational cost of the
Radix-2 FFT scheme is typically:
Number of (complex) multiplications = (NFDTD/2)log2(NFDTD NPxyzNP)
The storage requirements of the FFT are:
RAM required for FFT = 2NPxyzNPNF
Disk required for FFT = NFDTD NPxyzNP
IV. Linear Equation Methods
As an
alternative to fourier transform methods, this paper
presents two methods that overcome many of their limitations and have the added
advantages of flexibility and programming simplicity. Both methods are based on the solution of
linear equations. The first method,
called the two-equation two-unknowns (2E2U) method,
for use with single-frequency analysis is significantly more efficient than
fourier transform methods and can be applied effectively for an extremely broad
frequency range from the low kHz to high GHz and beyond. This method has the added advantage that for
many applications, it can be applied with virtually no memory or computational
requirement (beyond the FDTD requirements themselves). [15]
The second
method, called the N-equation N-unknown (NENU) method, is an extension of the
first method and can be used for multi-frequency analysis. In theory, this method minimizes
computational and memory requirements for any simulation. However, computer round-off errors limit its
application somewhat. Trade-off curves
are presented that show that this multi-frequency extension is the most
efficient method for up to about 40 frequencies, and that the single-frequency
method is preferable for larger numbers of frequencies. [21]
These two
methods are presented below.
a. Two Equations - Two Unknowns Method
The two-equations two-unknowns
(2E2U) method is a simple, direct method to obtain the magnitude and phase of a
sine wave in the time-domain based on writing two equations in two unknowns
(magnitude and phase) for the time-domain fields, and then solving them
directly for the magnitude and phase. At a given location in space, we can
write
A sin (wt1 + q) = q1
A sin (wt2 + q) = q2 (2)
where A is the magnitude, q is the phase angle, and w ( = 2 p F) is the
angular frequency. At two time steps, t1
and t2, the values q1 and q2 are obtained from
the FDTD simulation. These equations can
be solved for the unknowns, A and q, to give direct
relationships for these values:
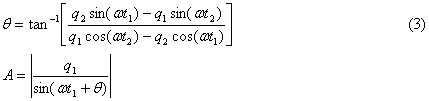
The choice of t1 and t2
depends on the simulation. For most FDTD
simulations the spatial resolution Dx is on the order of l / 10 to l /
100. For these simulations t1
and t2 can be the last two time steps of the simulation. For higher-resolution simulations the time
resolution is also high (Dt = Dx/2c), so q1 and
q2 are nearly equal if t1 and t2 are very
close. This results in errors due to
numerical round-off when calculating A and q. For these simulations, it is better to choose
t1 to be a few time steps (say, 50) before the end of the
simulation, and t2 to be the final time step such as was done in [6].
The equations in (3) can be
programmed one of two ways, depending on t1 and t2. The first is to store (or output to disk) the
value of q1 at time step t1, and then when the final time
step, t2, is reached, the values of A and q can be calculated. This is necessary if t1 and t2
are not subsequent time steps. An
alternate method of eliminating the memory requirement can be used when t1
and t2 are taken to be the last two time steps. For the final time step, q1 is
stored in a single location (not an array), then q2
is calculated from the last time step of the FDTD algorithm. This gives A and q which can be output to disk
or stored in the same locations as the fields used to compute them (remember
FDTD is now finished). This is then
repeated for each location.
The 2E2U method provides accurate
magnitude and phase calculations for simulations with clean, sine wave
output. Noise and DC offsets will cause
errors. Ramped sine excitations known
not to cause a DC offset should be used [22] or a pulse with a very smooth
turn-on [23]. Ramped sine excitations
have also been observed to reduce or eliminate numerical noise in FDTD
simulations [24].
The
computational requirements for this method are :
Number of
multiplications = 4NPNPxyz
The memory
requirements for this method are:
RAM required for 2E2U (storing
t1 timestep) = NPNPxyz
RAM required for 2E2U (using last timesteps) = 0
Disk required for 2E2U =
0
b. N-Equations N-Unknowns
The two-equations
two-unknowns method can be extended to multiple frequencies. In this case, N-equations are solved for
N-unknowns (NENU) which are the amplitude and phase at each frequency of
interest. This requires samples at 2N
time steps and results in the following equations for two frequencies:
A1 sin (w1t1
+ q1) + A2
sin (w2t1
+ q2) = q1
A1
sin (w1t2
+ q1) + A2
sin (w2t2
+ q2) = q2 (4)
A1 sin (w1t3
+ q1) + A2
sin (w2t3
+ q2) = q3
A1
sin (w1t4
+ q1) + A2
sin (w2t4
+ q2) = q4
This can be extended to multiple
frequencies where the source is a sum of sine waves:
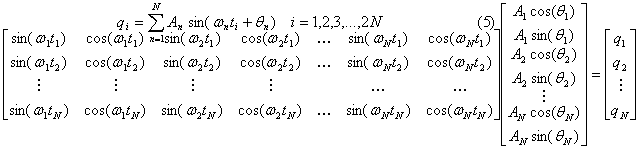
Using
trigonometric identities on the sine function, this can be broken into a matrix
equation which can be solved for functions (Ancos(qn) ) of An
and qn .
A standard matrix solution method
such as Gaussian elimination is used to obtain the vector of functions An
sin or cos(qn).
The unknowns An and qn are then found from these
functions.
This
form of the NENU method requires a multi-frequency source in the form of (5),
which does not utilize methods such as sine wave ramping to prevent high
frequency transients or DC offsets.
These specialized ramps could be included in the source type, and the
same solution method could be followed by changing the specifics of the matrix
above.
In
theory, the NENU method provides an exact conversion from time to frequency
domain. In practice, however, the matrix
can be ill-conditioned because of computer round off error. This happens when the cosine and sine samples
become very close together so that they are numerically indistinguishable when
the time samples (t1, t2, t3, etc.) are too
close together, when a very large number of frequencies are involved, or when
the frequencies are too close together.
There is a also a problem when their relative
magnitudes of the source are several orders of magnitude different (which can
be prevented simply by scaling magnitudes AFTER time-do-frequency domain
calculations). This paper discusses each
of these problems and the efficiency tradeoffs for solving them.
As an example
of the application of the NENU method solutions were computed for twenty-five
different frequencies as a function of the spacing of the time samples (t2
= t1 + nDt). The frequencies are evenly-spaced from 0.1 to
1 MHz, and have equal magnitudes. The time
resolution Dt = Dx / 2c, where Dx is the spatial resolution
of the FDTD grid, and Dx = lmin / 20. Figure 1 shows the inverse of the condition
number. A large condition number (small
inverse) indicates a poorly-conditioned matrix.
The spikes seen in the inverse condition number indicate sample spacings
providing most accurate matrix solutions.
These are clearly sporadic. In
particular, note that simply taking time samples that are far apart does not
ensure accurate matrix solution. Figure
2a shows the maximum error in the computation of amplitude when using the
simple Ax=b form and Gaussian elimination as a function of sample spacing.
Errors of less than 1% are obtained when samples are spaced at least seven
samples apart, and low errors are obtained for all of the sample spacings that
provide high inverse condition numbers in Figure 1. A difficulty with using sample spacings that
are far apart is that additional FDTD time steps must be run beyond convergence
of the solution. Improvements can be made. The singular value decomposition (SVD) is
commonly used to solve ill-conditioned matrices by removing or reducing the
near-zero eigenvalues. Figure 2b shows
the maximum error in the computation of the magnitude using the Singular Value
Decomposition and related psuedo-inverse to solve the matrix equation. Using
SVD provides accurate calculations (less than 1% error) for all time sample
spacing. This enables calculations of
magnitude and phase of twenty-five frequencies using the last fifty converged
time steps of the FDTD simulation.
The accuracy advantage of using the SVD
becomes more pronounced as the number of frequencies increases. For instance, it was found that for 100
frequencies evenly-spaced from 0.1 to 1MHz, the SVD can provide calculations
with less than 1% error for sample spacings greater than four, whereas the
direct method without SVD requires at least a spacing of twenty-one
samples.
The computational requirements for
the N-equation N-unknown method using Gaussian elimination are [25] :
Number of
multiplications = 9NDFDTDNxyz
+ NPxyzNP (2NF )3
/3
The
computational requirements for the N-equation N-unknown method using SVD are
[26] :
Number of
multiplications = 9NDFDTDNxyz
+ 12NPxyzNPNF3
The memory
requirements for NENU are:
RAM required for NENU = (2 NF)2 NPxyz NP
Disk required for NENU = 0
It is clear that there is a substantial tradeoff between accuracy and
efficiency in the NENU method using Gaussian elimination or SVD. This will be examined for specific applications
below.
V. Applications
This section outlines several
applications of time-to-frequency domain calculations and the computational
aspects surrounding them. Four specific
applications will be considered. These
are computation of (a) antenna impedance,
(b) radiation pattern, (c) absorbed power or field distributions such as for
cellular telephone analysis, and (d) low frequency high resolution simulations
such as analysis of a millimeter resolution model of the human body in the
presence of a 60 Hz field.
The computational
requirements for the different methods of converting from time to frequency
domains are compared in Table 1. Their
relative efficiency depends on the number of frequencies of interest and the
number of parameters and locations where the conversions must be made. This is application dependent. Figure 3 shows the effect of frequency for an
application where a large number of time-to-frequency domain conversions are
required (such as analysis of cellular telephones). For a small number of frequencies (1 or 2),
the 2E2U method is the most efficient.
For a larger number of frequencies (up to about 37) the NENU method
using gaussian elimination is most efficient.
For more frequencies than that, the DFT is more efficient because it
does not require additional FDTD time steps.
This figure also emphasizes the importance of choosing the most
efficient method for the application, because of the extremely large
computational burden of computing magnitude and phase as compared to simply
running the FDTD simulation.
The relative efficiency
of the methods depends strongly on the application. Table 2 summarizes the computation and memory
requirements of the various methods for the applications discussed below.
a. Impedance Calculations
Impedance calculations
require relatively few time-to-frequency domain calculations. Impedance is generally computed as Z = V / I , where Z,V,I are complex values. The voltage is found from the line integral
of the electric field (requiring one electric field component), and the current
is found from the closed contour integral of the magnetic field (requiring four
magnetic field components) around the electric field that is used to find the
voltage [1,8]. Thus, only five
time-to-frequency domain conversion may be required to compute impedance. Table 2 shows the relative computation and
memory requirements for an example that has the following parameters:
Number of Frequencies NF = 1 and 25
Number of Parameters NP = 5
Number of FDTD cells Nxyz = 100 x 100 x 100
Number of FDTD time steps NFDTD = 2000 (typical for low-Q
simulations)
From Table 2, it is clear that the 2E2U and NENU methods are more
efficient than the DFT for single frequency calculations. For multiple frequencies, the DFT or NENU
should be used, as the expense of additional FDTD simulations would negate the
efficiency of the 2E2U method. For an
application such as impedance calculations where few field components require
time-to-frequency domain conversions, all of the methods are relatively
inexpensive compared to the FDTD simulation itself. Storage is minimal for all of these methods
for this application. Even the FFT with commercial software could be used for
this application.
b.
Radiation Pattern Calculations
Calculation of antenna
radiation patterns requires a moderate number of time-to-frequency domain
conversions. Equivalent surface currents
are found by integrating the electric and magnetic fields tangential to a
cubical surface surrounding the radiator and transformed to the far-field in
either the time or frequency domains [16].
If they are converted to the frequency domain and then transformed to
the far field (following the method of Van Bladel [8,27]),
four tangential electric and magnetic field components are required on each of
six surfaces surrounding the antenna.
For an example where the total FDTD space is 100 x 100 x 100 cells, the
radiation pattern may be taken five cells inside the boundary, so each of the
six surfaces is 90 x 90 cells. This
gives the number of parameters NP = (4 field components) (6 surfaces) (90 x 90
cells) = 194 400. Table 2 shows the
relative computational requirements for this example:
Number of frequencies NF = 1 and 25
Number of Parameters NP = 194 400
Number of FDTD cells Nxyz = 100x100x100
Number of time steps NFDTD = 2000 (typical low-Q
example)
For this example, which
has a moderate number of time-to-frequency domain conversions (two dimensional
surfaces rather than three dimensional volumes), the 2E2U method would again be
most efficient for single frequency calculations. NENU and DFT would be most efficient for
multiple frequency calculations. The
2E2U and NENU methods would require less storage than the DFT method, although
this storage is still small compared with the overall FDTD simulation
requirements.
c.
Field or Power Distribution
Field, power or current
density distributions are commonly calculated with the FDTD method for analysis
of safety guidelines or for showing color plots of these distributions. Commonly they are done for every point in a
three-dimensional grid and therefore require a very large number of
time-to-frequency domain conversions. Examples include bioelectromagnetics and
medical imaging and inversion problems, [1-4,28] and
geophysical applications [29]. In order
to find the complete electric field distribution, for instance, this would
require time-to-frequency domain conversions for three field components for
every cell in the simulation. The
relative computational requirements of the various methods are given in Table 5
using the values given below:
Number of Frequencies NF = 1 and 25
Number of Parameters NP = (3 fields) (Nxyz cells) = 3 000
000
Number of FDTD cells Nxyz = 100 x 100 x 100 = 1 000
000
Number of FDTD time steps NFDTD
= 2000
From Table 2, the
significance of the savings that can be obtained using the 2E2U or NENU methods
becomes more apparent for this application.
The DFT requires about as much computational time and as much storage as
the FDTD simulation itself. This means
that half of the system resources are being dedicated to the time-to-frequency
domain transformation. The 2E2U method
provides a significant improvement for single-frequency simulations, five
orders or magnitude less computation and virtually no storage requirement. This frees up system resources for larger
problem sizes rather than larger post-processing applications. The NENU method is slightly more efficient
than the DFT for multiple frequency simulations up to about 35
frequencies. This is an approximation
and would need to be analyzed for the specific array of frequencies of
interest.
In a problem of this
size, the 2E2U method would not necessarily be the most efficient method, however it has potential application because of its
ability to compute the frequency domain fields with virtually no memory. Many realistic simulations are constrained
more by memory than computer time.
d.
Low Frequency High Resolution Simulations
Low frequency high
resolution simulations present a peculiar problem for time-to-frequency domain
conversions that is solved using the 2E2U method. Until recently, the FDTD method was limited
to applications where the simulation could be completed for at least one half
cycle of the lowest frequency in the wave.
This precluded low frequency analysis of high resolution models. For instance, analyzing a 6mm resolution
model of the human body at 60 Hz would require 1.7 x 109 time steps
per cycle of the wave [6]. The use of
pulsed FDTD with the fourier transform and frequency scaling [5,30] and the 2E2U method [6,31,32] have extended the range
of this method to very low frequencies (down to 60 Hz). Both of these methods take
advantage of the fact that the FDTD simulation actually converges in a moderate
number of time steps (say 2000), and that the only difficulty is obtaining the
magnitude and phase data from far less than a single cycle of the fields. This is done using the 2E2U method, and is
shown to be highly accurate when compared to analytical and measured data. [6,31,32] . This has allowed direct calculation of the
magnitude of 60 Hz fields within the human body with modeled resolution of
2mm. Other methods simply could not
solve this problem, so the 2E2U method has been critical to the understanding
of these low frequency fields.
Figure 4 shows the application of
the 2E2U method to geophysical simulations.[32] This simulation analyzes a typical nickel
sulfide deposit in the Kambalda formation in
c.
Conclusions
and Summary
Figure 3
shows the relative cost of the fourier transform, 2E2U
and NENU methods for an application requiring a large number of
time-to-frequency domain conversions. For a single frequency, the 2E2U method is
most efficient. For up to about 40
frequencies, the NENU method is most efficient.
Memory is
also a tradeoff for these methods. As
noted in Table 1, the DFT must store a complex value (equal to two real values)
for every location and parameter of interest.
The 2E2U can completely eliminate this requirement if the sampling
resolution is sufficient to allow computation of magnitude and phase from the
final two time steps of the simulation.
The NENU method must store the matrix that is (2 NF)2
where NF is the number of frequencies for each location and parameter of
interest. These values would generally
be written to disk, with final solution being done as a post-processing step,
but this may be prohibitively expensive for some applications. The optimal method to use depends on the size
of the problem and number of time-to-frequency domain conversions
required.
For
applications with relatively few time-to-frequency domain conversions such as
antenna impedance calculations, all methods could be used. The 2E2U and NENU methods would be the most
efficient. For applications with a
moderate number of time-to-frequency domain conversions such as antenna
radiation pattern calculations, the 2E2U method would be most efficient for
single frequency studies, and the DFT or NENU methods would be most efficient
for multiple frequency studies. For
applications with a large number of time-to-frequency domain conversions such
as computation of complete field or power distributions, efficiency of the
methods is critical. The 2E2U method is
clearly the most effective for single frequency calculations, and the NENU
method and DFT would be used for multiple frequency simulations, depending on
the number of frequencies being considered.
The 2E2U method is also critical for use in FDTD simulations that are
low frequency and high resolution (ultra-high resolution with respect to
wavelength.
The
time-to-frequency domain conversion methods described in this paper give a good
range of options to choose from for different applications of FDTD
simulations. Choosing the optimal method
can lead to huge advantages of code efficiency and an increase in the overall
problem size that can be simulated with given computer resources. The DFT, 2E2U, and NENU methods are all good
choices for FDTD time-to-frequency domain conversions.
References
[1]
O. P. Gandhi, G. Lazzi, and C. M. Furse, "Electromagnetic Absorption in
the Human Head and Neck for Mobile Telephones at 835 and 1900 MHz," IEEE Transactions on Microwave Theory and
Techniques, Vol. 44, October 1996, pp. 1884-1897
[2]
M. Okoniewski, M.A. Stuchly, "A Study of the Handset Antenna and Human
Body Interaction,"
IEEE Transactions on Microwave Theory and
Techniques, Vol. 44, October 1996, pp. 1855-1864
[3] M. A. Jensen and Y. Rahmat-Samii, "EM Interaction of Handset
Antennas and a Human in Personal Communication," Proc. IEEE, Vol. 83, pp. 7-17, 1995.
[4] P. J. Dimbylow and S. M.
Mann, "SAR Calculations in an Anatomically Based Realistic Model of the
Head for Mobile Communication Transceivers at 900 MHz and 1.8 GHz," Physics in Medicine and Biology, Vol.
39, pp. 1537-1553, 1994.
[5] O.P. Gandhi, J.Y. Chen,
"Numerical Dosimetry at Power Line Frequencies Using Anatomically-Based
Models," Bioelectromagnetics
Supplement 1992, pp. 43-60
[6] C. M. Furse, J. Y. Chen,
and O. P. Gandhi, "Calculation of Electric Fields and Currents Induced in
a Millimeter-Resolution Human Model at 60 Hz Using the FDTD Method," Bioelectromagnetics, 19(5), 1998,
pp.293-299
[7] O. P. Gandhi, Y. G. Gu,
J. Y. Chen, and H. I. Bassen, "Specific Absorption Rates and Induced
Current Distributions in an Anatomically Based Human Model for Plane-Wave
Exposure," Health Physics, Vol.
63, pp. 281-290, 1992.
[8] G.Lazzi, S.S. Pattnaik,
C.M. Furse, O.P. Gandhi, "Comparison of FDTD-Computed and Measured
Radiation Patterns of Commercial Mobile Telephones in Presence of the Human
Head," IEEE Trans. Antennas and
Propagation, June 1998, pp.943-944
[9] A. Taflove,
K. Umashankar, "Review of FD-TD Numerical Modeling of Electromagnetic Wave
Scattering and Radar Cross Section," Proc.
IEEE, Vol.77, pp. 682-698, May 1989
[10] T. Shibata,
T. Hayashi, T. Kimura, "Analysis of Microstrip Circuits Using
Three-Dimensional Full-Wave Electromagnetic Field Analysis in the Time
Domain," IEEE Trans. Microwave
Theory and Techniques, June 1988, pp. 1064-1070
[11] J.C.
Olivier, "Mutual Coupling Between Waveguide Apertures Mounted on a Common
Conducting Surface Using a Time- and Fourier-Gated Pulsed FDTD Method," IEEE Trans. Microwave Theory and Techniques,
Feb. 1993, pp. 290-297
[12] A.C.
Cangellaris, M. Gribbons, G. Sohos, "A Hybrid Spectral/FDTD Method for the
Electromagnetic Analysis of Guided Wave Structures," IEEE Microwave and Guided Wave Letters, Oct. 1993, pp. 375-377
[13] C.M. Furse,
S.P. Mathur, O.P. Gandhi, "Improvements to the Finite-Difference
Time-Domain Method for Calculating the Radar Cross Section of a Perfectly
Conducting Target," IEEE Trans.
Microwave Theory and Techniques, Vol. MTT-38, No. 7, July 1990, pp. 919-927
[14] Z. Bi,
Y.Shen, K.Wu, J.Litva, "Fast Finite-Difference Time-Domain Analysis of
Resonators Using Digital Filtering and Spectrum Estimation Techniques," IEEE Trans. Microwave Theory and Techniques,
pp. 1611-1619, 1992
[15] C.M. Furse, "Use of
the Finite Difference Time Domain Method for Broad Band Calculations of
Electromagnetic Scattering and Absorption from Large Heterogeneous
Objects," Ph.D. dissertation,
[16]
A.Taflove, Computational Electrodynamics: The Finite-Difference Time-Domain
Method, Artech House, 1995
[17]
K.S. Kunz, R.J. Luebbers, The Finite Difference Time Domain Method for
Electromagnetics, CRC Press, Boca Raton, FL, 1993
[18]
S. Haykin, Digital Communication, John Wiley and Sons, 1988
[19]
C.M. Furse, O.P. Gandhi, "Why the DFT is faster than the FFT for
time-to-frequency domain conversion," IEEE
Microwave and Guided Wave Letters , Vol. 6, No. 10, 1995, pp. 326-328
[20]
A. Dutt and V. Kokhlin, "Fast Fourier Transforms for non-equispaced
data," SIAM J. Sci. Comput.,
Vol. 14, pp. 1368-1393, 1993
[21]
C.M. Furse, "Faster than Fourier -- Ultra-Efficient Time-to-Frequency
Domain Conversions to FDTD Applied to Bioelectromagnetic Dosimetry," ACES Symposium
(Dec. 3, 1997) ,
[22]
C.M. Furse, D.H. Roper, D.N. Buechler, D.A. Christensen, C.H. Durney, "The
Problems and Treatment of DC Offsets in FDTD Simulations," IEEE Transactions on Antennas and
Propagation, October 2000
[23]
D.S. Katz, E.T. Thiele, A. Taflove, “Validation and Extension to Three
Dimensions of the Berenger PML Absorbing Boundary Condition for FD-TD Meshes,” IEEE Microwave and Guided Wave Letters , 4(8), pp. 268- 270, August, 1994
[24]
Buechler DN, Roper DH, Christensen DA, Durney CH (1995): Modeling sources in the FDTD formulation and
their use in quantifying source and boundary condition errors. IEEE Trans. Microwave Theory
and Techniques 43(4).
[25] A. Ralston, P. Rabinowitz, "A First Course in Numerical Analysis," McGraw-Hill, 1978, p.417
[26] G.H. Golub, C.F. Van Loan, Matrix Computations, second edition, Johns Hopkins University Press, 1989, p. 239
[27]
J. Van Bladel, Electromagnetic Fields, Hemisphere Publishing Co., 1985,
pp. 254-258
[28]
A.Taflove, editor, Advances in Computational Electrodynamics, Artech
House, 1998
[29] T.Wang, and G.W.Hohmann, "A finite-difference time-domain solution for three- dimensional electromagnetic modeling," Geophysics, 58, 797-809, 1993
[30] J.Y.Chen and O.P. Gandhi OP, "RF currents induced in an anatomically-based model of a human for plane-wave exposures 20-100 MHz," Health Physics, Vol. 57, pp. 89-98, 1989
[31] T. Dawson, K. Caputa, M.A. Stuchly, "High-resolution organ dosimetry for human exposure to low-frequency electric fields," IEEE Trans. Power Delivery, accepted for publication
[32] D.Johnson, C.Furse, A.C.Tripp, "FDTD Modeling of
the Borehole EM Response of a Conductive
[33] M. R. Zunoubi, N. H. Younan, J. H.
Beggs, and C. D. Taylor, "FDTD Analysis of Linear Antennas Driven From a
Discrete Impulse Excitation," IEEE Trans.Electromagn.
Compat., vol. 39, pp. 247-250, Aug. 1997.