ECE 5340/6340
The Finite Difference
Frequency Domain Method Applied to Waveguides
The FDFD Method has been used to solve Laplace's and Poisson's Equations:
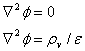
The 5-point stencil is used to evaluate the Laplacian
Operator (Ñ2):
![]()
This can also be used to evaluate the Scalar Wave Equation (Helmholtz
Equation):
![]()
Where
f=Ez for TM modes
f=Hz
for TE modes
and all fields vary as ej(wt-bz)
k is the wave number and k2 = w2me-b2
The propagation constant is : b=(w/ce)Ö(1 - (fc / f)2) rad/m
Waveguides have several different modes. The mode number indicates the number of half-sine variations of f in the x-y directions. For instance , a TM10 mode would have 1 half sine wave of change along the x-direction (Ez is zero on the x-edges and maximum in the center. It is constant in the y-direction). Multiple modes can exist in a waveguide at a given time. The higher the frequency, the more modes can propagate.
A waveguide's mode is determined by two things:
a) The frequency
b) The feed system (which must be able to establish a given mode)
The frequency must be ABOVE the cutoff frequency fc of a given mode in order for the mode to propagate.
The field distribution in the waveguide can often be found as an analytical solution of the Helmholtz equation applying the boundary conditions. But if it cannot be found analytically, FDFD is a good method of solving this.
The steps to apply the FDFD method to the Helmholtz Equation:
1) Divide the cross section of the waveguide (x-y plane) into a mesh
2) Apply 5-point difference formula
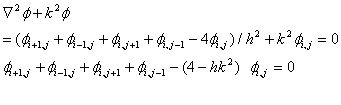
Boundary Conditions
TM = transverse magnetic: Ez is tangential to metal
boundaries
Use
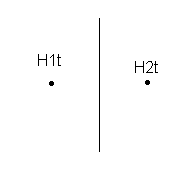
TE =transverse electric: Hz is tangential to metal boundaries
n X (B1 - B2) = Js = 0
H1t = H2t
Derive SOR:
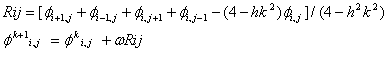
But we also don't know k.
So, we GUESS k, and iterate 3 or 4 times, then apply the Raleigh Formula to find k:
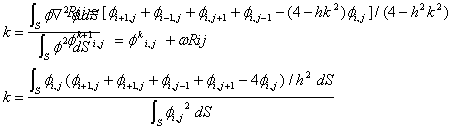
Find the surface integrals using numerical integration.
Use this new value of k and continue updating f.
Continue until k converges. f will also be converged.